注：本篇文章原用于提交笔者高中的研究性学习报告，由于时间仓促与水平所限，不能完全保证正确性，文章水平也只是保持高中范围内的“点到为止”。请读者保持独立思考，也希望各位能在发现错误后不吝指正。以下为删除小组实验部分、仅仅保留理论部分后的原文，供各位在读高中生以及各界人士参考。

电在输送时一般都是以交流电输送的。高中实验室却一般使用直流电，这就产生了一个问题——如何将电网中的交流电转换为实验室所用直流电？

一、交流电与直流电的区别

要想转换，首先需要理解交流电与直流电的不同。

在直流电路中，除换路瞬间，电流、电压的方向不会随时间而改变。而在交流电路中，电压与电流会随时间改变。本文中交流电均指正弦波，即按照正弦规律周期性变化的交流电(当然也可以说是按余弦规律变化，方便起见本文中统一使用正弦表示)。

正弦电压和电流等物理量，被统称为正弦量。正弦量的三要素分别是频率 ff (或周期 TT )、幅值 ImI_m 及 UmU_m (或有效值 II 及 UU )、初相位 ψ\psi 。

一般使用小写字母 uu 、 ii 等表示瞬时值，有效值用大写字母 UU 、 II 等表示，幅值(指瞬时值的最大值)则在大写字母的右下方标记 mm 。一般来说，交流电中的电压与电流可用下式表示：

{u=Umsin(ωt+ψ1)i=Imsin(ωt+ψ2)\begin{equation} \begin{cases}u=U_msin(\omega t+\psi_1) \\ i=I_msin(\omega t+\psi_2) \end{cases} \end{equation}

方便起见，本文中的初相位均默认为0。

有效值的定义，则是这样的：对于交流电与直流电，相等时间内通过同一电阻而产生的热效应相等，那么它们的安培值是相等的。亦即：

∫0TRi2dt=RI2T\int_{0}^{T}Ri^2\,dt=RI^2T

代入正弦电流表达式计算之后，可得 Im=2II_m=\sqrt2 I 。相应地也能得到 Um=2UU_m=\sqrt2 U 。

另外还有一个指标：平均值。以电压为例，电压的平均值即为电压瞬时值的累加与被累加时间段时长的数值的比值，并以 UOU_O 表示（注意这里的下标是字母 OO

而不是数字0）。在周期性变化的直流电中，通常取一个周期内的平均值作为电压的平均值。根据定义可得：

UO=1T∫T0udtU_O=\frac{1}{T}\int_{T}^{0}u\, dt

二、半波整流

二极管具有单向导电性。因此很容易就想到二极管是组成整流电路的关键元件。所需整流交流电的波形如图2.1所示。

图2.1

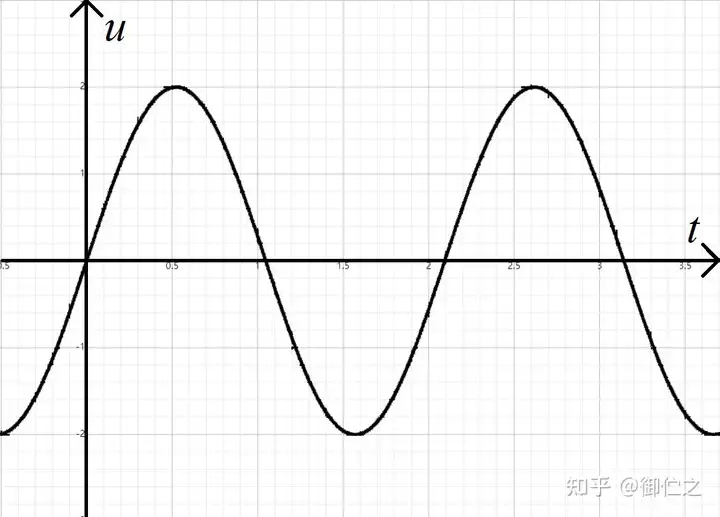
我们首先作出了如图2.2所示电路。

图2.2

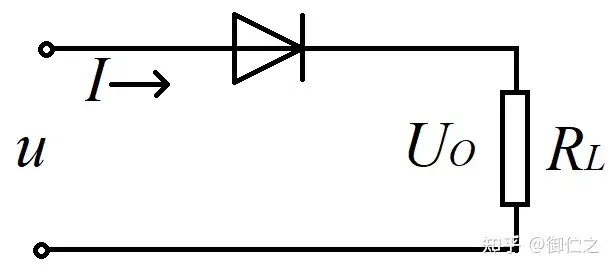
这样就能整流输出一半的波形，而这样的整流就被称为“半波整流”。整流之后形成的波形如图2.3所示。

图2.3

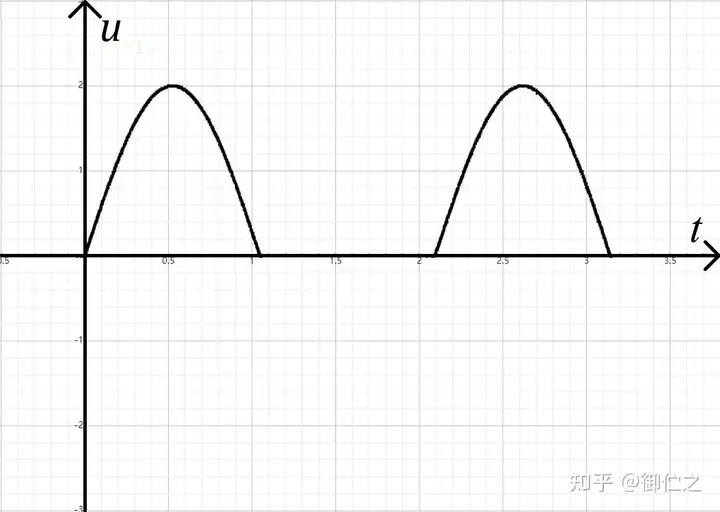
根据平均值的计算，此时输出的平均电压为：

UO=1T∫0T2Umsin(ωt)dt=2Uπ≈0.45UU_O=\frac{1}{T}\int_{0}^{\frac{T}{2}}U_msin(\omega t)dt=\frac{\sqrt2U}{\pi}\approx 0.45U

可见此时输出电压很低，不到原交流电有效值的一半，有很大的损失。因此，我们决定寻找“使损耗尽可能低的整流电路”。

三、全波整流(桥式)

与半波整流相对地，我们需要思考如何能够将负方向的正弦量也利用起来，使其被转换为正方向，让横轴以下正弦量翻转至横轴之上。我们一开始设计了图3.1的电路：

图3.1

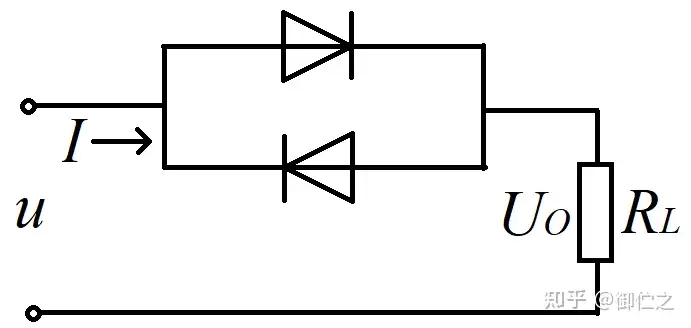
当正弦波方向为正时，电流流经上半部分而被下部分阻挡，方向为负时电流流经下部分而被上部分阻挡。但组内成员及时制止了这一错误：这样输出的电压，原正方向依旧为正，原负方向依旧为负，未起到整流作用。

因此如何有效整流成为了我们的下一步思考方向。据此我们查阅资料，设计了如图3.2的桥式电路。

图3.2

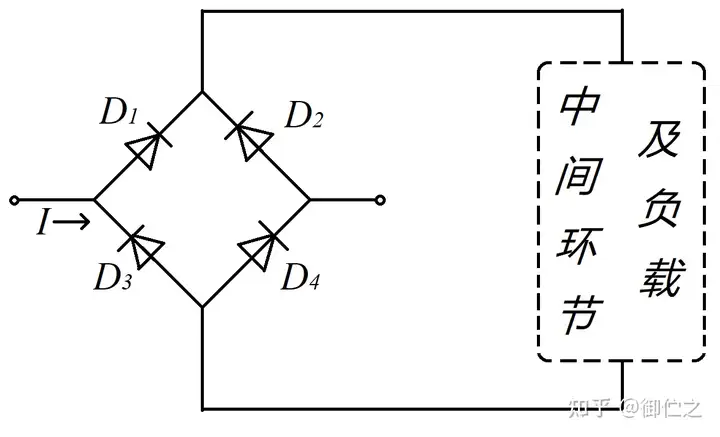
当正弦量方向为正时， D1D_1 、 D4D_4 导通而 D2D_2 、 D3D_3 截止，方向为负时D2D_2 、 D3D_3导通而D1D_1 、 D4D_4截止。这样流经负载的电流方向就一样了。

这一次整流之后形成的波形，如图3.3。

图3.3

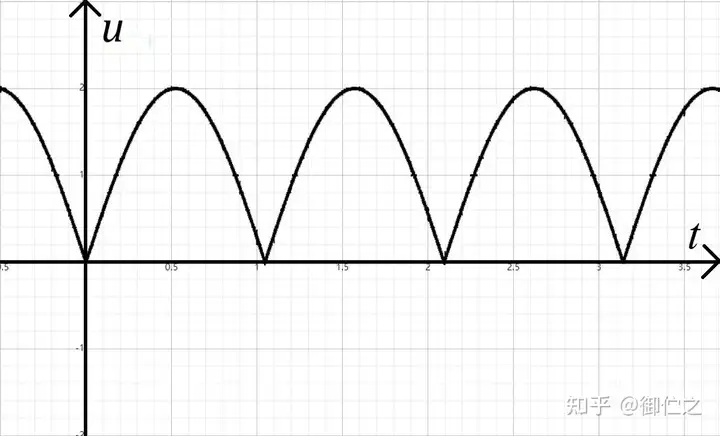
这样，我们就得到了方向单一的脉冲直流电。计算输出电压平均值易得：

UO=ωπ∫0πωUmsin(ωt)dt=22Uπ≈0.9UU_O=\frac{\omega}{\pi}\int_{0}^{\frac{\pi}{\omega}}U_msin(\omega t)dt=\frac{2\sqrt2U}{\pi}\approx 0.9U

可以说，这一次整流的效果已经能够使人满意，其损耗大约是原有效值的百分之十。

四、滤波

根据上述，电压随时间变化的函数此时可以写成：

u=|Umsin(ωt)|={Umsin(ωt),t∈[0,πω]−Umsin(ωt),t∈[πω,2πω]u=\left| U_msin(\omega t) \right|= \begin{equation} \begin{cases}U_msin(\omega t),t\in\left[ 0,\frac{\pi}{\omega} \right] \\ -U_msin(\omega t),t\in\left[ \frac{\pi}{\omega},\frac{2\pi}{\omega} \right] \end{cases} \end{equation}

将其展开为FourierFourier 级数：

an=2π∫0πUmsin(ωt)cos(nt)dt=Umπ∫0πsin(ω+n)t+cos(ω−n)tdt=Umπ[−cos(ω+n)tω+n−cos(ω−n)tω−n]0π=Umπ[−1−cos(ω+n)πω+n−1−cos(ω−n)πω−n]a_n=\frac{2}{\pi}\int_{0}^{\pi}U_msin(\omega t)cos(nt)\,dt\\ =\frac{U_m}{\pi}\int_{0}^{\pi}sin(\omega +n )t+cos(\omega-n)t\,dt\\ =\frac{U_m}{\pi}\left[ -\frac{cos(\omega +n )t}{\omega +n} -\frac{cos(\omega -n )t}{\omega -n}\right]_0^\pi\\ =\frac{U_m}{\pi}\left[ -\frac{1-cos(\omega +n )\pi}{\omega +n} -\frac{1-cos(\omega -n )\pi}{\omega -n}\right]

为研究方便，这里取 ω\omega 为奇数(取偶数也会有类似的过程)，那么：

an={−4Um(n2−1)π,n=2,4,6...0,n=3,5,7...a_n= \begin{equation} \begin{cases}-\frac{4U_m}{(n^2-1)\pi},n=2,4,6... \\ \,\,\,\,\,\,0\,\,\,\,\,\,,n=3,5,7... \end{cases} \end{equation}

又分别计算得到 a0=4Umπa_0=\frac{4U_m}{\pi} ， a1=0a_1=0 。于是：

u=a02+∑n=1+∞ancosnωt=4Umπ(12−13cos2ωt−115cos4ωt−135cos6ωt−...)u=\frac{a_0}{2}+\sum_{n=1}^{+\infty}{a_ncos\,n\omega t}=\\ \frac{4U_m}{\pi}\left( \frac{1}{2}-\frac{1}{3}cos\,2\omega t-\frac{1}{15}cos\,4\omega t-\frac{1}{35}cos\,6\omega t-... \right)

由此可见，直流分量为 2Umπ\frac{2U_m}{\pi} ，最低次谐波的幅值为 4Um3π\frac{4U_m}{3\pi} ，所有谐波分量(总称为纹波)均叠加于直流分量之上。高次谐波具有极高频率，会对电器造成很大损害，因此需要“滤波”，即将高次谐波滤去。

我们便开始着手研究图3.2中虚线框内的中间环节。整流后的波形周期性波动，其实就是能量的脉冲变化。因此要想使得波形更加平滑，应当让能量有一个“缓冲”的过程。于是我们选择了电容，因为它能够储能与放能。

我们首先研究了 RCRC 电路的全响应，即电源激励与电容的初始状态均不为零的响应。电路图如图4.1。

图4.1

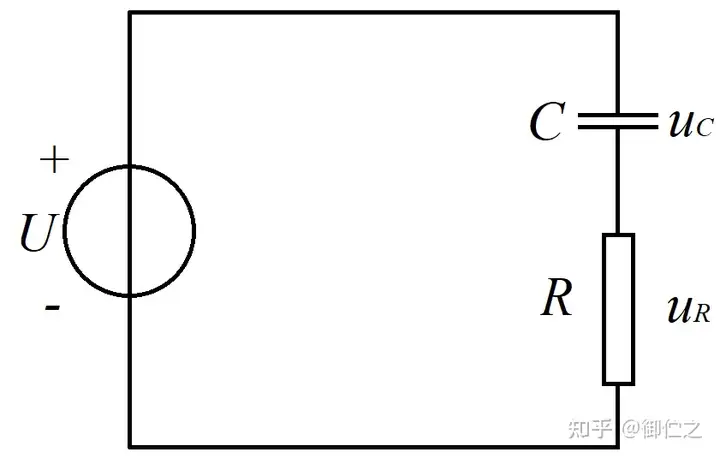
根据 Kirchhoff′sVoltageLawKirchhoffs\,\,\, Voltage\,\,\, Law

，应有如下微分方程：

U=uR+uC=Ri+uC=RCduCdt+uCU=u_R+u_C=Ri+u_C=RC\frac{du_C}{dt}+u_C

分离变量：

dt=RC⋅duCU−uCduCdt=RC\cdot\frac{du_C}{U-u_C}\,du_C

两边积分：

t=RC∫duCU−uCduC=−RC⋅ln(U−uC)+const.t=RC\int\frac{du_C}{U-u_C}\,du_C=-RC\cdot ln(U-u_C)+const.

反解方程：

uC=U−econst.−tRC=U−econst.RC⋅e−tRCu_C=U-e^{\frac{const.-t}{RC}}=U-e^{\frac{const.}{RC}}\cdot e^{\frac{-t}{RC}}

代入初始条件 uC|t=0=U0u_C |_{t=0}=U_0 ：

econst.RC=U−U0e^{\frac{const.}{RC}}=U-U_0

代回原方程即得 uC=U+(U0−U)e−tRCu_C=U+(U_0-U) e^{\frac{-t}{RC}} 。其中 U0U_0 为电容的初始状态。由此可得，当电容初始电压 U0U_0 大于电压源电压 UU 时，电容处于放电状态且电压以指数规律下降；当 U0<UU_0<U 时，电容处于充电状态且电压以指数规律上升。

另外，量纲分析之:

RC=[L2MT−3I−2]⋅[L−2M−1T4T2]=[T]RC=\left[ L^2MT^{-3}I^{-2} \right]\cdot \left[ L^{-2}M^{-1}T^4T^2 \right]=[T]

即的 RCRC 量纲为时间，并且其值为常数，因此被称为 RCRC 电路的时间常数并以 τ\tau 表示。

据此，我们设计了虚线框中的电路，如图4.2。

图4.2

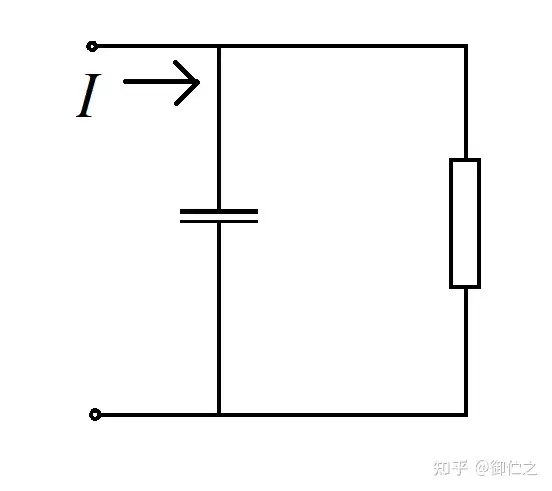
这个滤波电路所输出的波形如图4.3。

图4.3

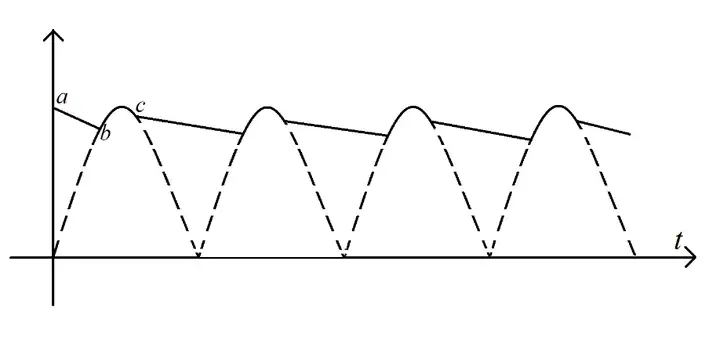
在 abab 段，整流后的电压 uu 正从 00 升至 UmU_m ，而电容器电压 uCu_C 正从 UmU_m 开始指数规律下降，即 u<uCu<u_C ，因此在图4.2电路中由电容为电阻(负载)提供电压。到达 bb 点时，u=uCu=u_C，之后在 bcbc 段u_C">u>uCu>u_C，因此由整流电压向4.2电路整体提供电压，此时电容器进入充电状态，与整流电压共进退（准确来说，电容充电时的外部电阻为桥式整流的导通部分电阻与负载电阻的并联，由于导通电阻极小所以其并联电阻极小。根据 τ=RC\tau=RC ，此时的时间常数也极小，因此充电时电容电压变化极快，几乎追平整流电压）。整流电压达到最大值 UmU_m 后开始下降，随后再次由电容放电为负载提供电压。周而复始便形成这样的波形。

肉眼可见地，电的波动变小了，事实上也确实滤去了高次谐波。到此，滤波的问题已经基本解决。

五、稳压

考虑到电网中的交流电会出现幅值的波动，可能会将电路击穿，因此我们决定再增加一个“稳压”的环节。

齐纳二极管具有十分特殊的性质。当它处于反向电压中时，极大的电流增量只能引起很小的电压变化。因此齐纳二极管又被称为稳压管，是稳压环节的不二之选。设计电路如图5.1。圆角矩形所包含处即为并联式稳压电路。

图5.1

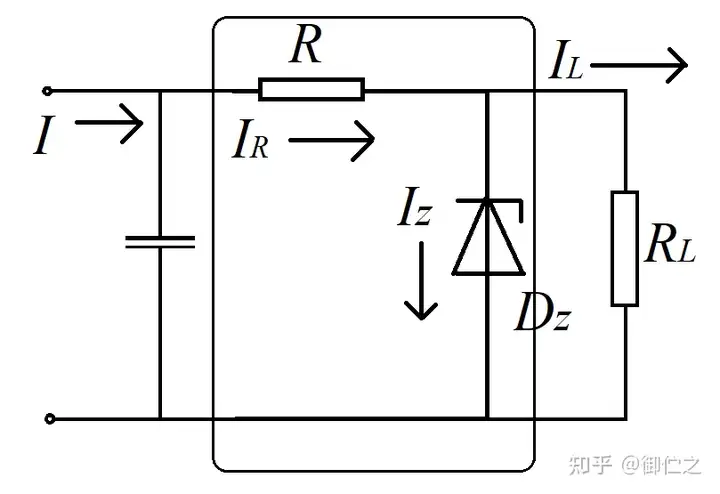
当外电路电压变大时，首先会引起电容器两端电压的增加，进而导致稳压管两端电压升高。电压的波动会导致流经稳压管的电流剧增。根据 Kirchhoff′sCurrentLawKirchhoffs\,\,\, Current\,\,\, Law ，可以得到 IR=IZ+ILI_R=I_Z+I_L ，所以流经限流电阻的电流也会增加。又根据欧姆定律得到 UR=IRRU_R=I_RR ，说明 RR 两端电压升高。又因为 RR 与 DZD_Z 的串联与电容并联， RR 电压的升高便会造成 DZD_Z 电压的下降。负载 RLR_L 与 DZD_Z 并联，意味着负载端电压也会下降。这样，负载电压就会大致回到原先水平。

若外电路电压变小，也会有类似的过程。

事实上，不止是能够在外电压变化时稳压，当负载变化的时候，稳压电路也会起到稳压作用。

六、变压

但依旧存在一个问题，国家电网中的电是220V高压，实验室所用直流电一般都在安全电压及以下。这就涉及到变压。变压环节应当设置在整流前。不过这与本文所讨论问题没有太大关联，因此不再赘述。

七、总电路

在逐个环节分析完后，我们绘制了如图7.1的总电路。

图7.1

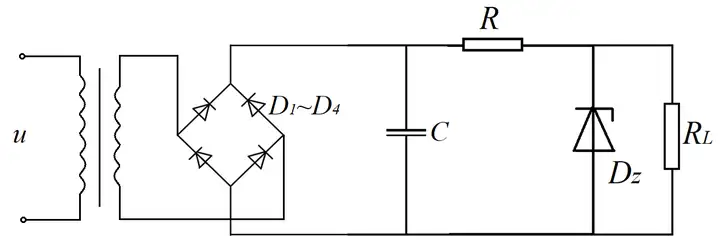
至此，我们完成了交流电转换直流电的所有理论环节。接下来，小组成员进行了实验。

八、实验

（实验部分已删除）

至此，所有环节结束。

小组成员：YZZ、F**、L**、L**、X**、W**