关键是：电容两端的电压不允许突变。所以当接通电源瞬间，电容两端的电压等于零，然后电压按指数规律上升，直到进入稳态。进入稳态后的电容相当于断路，也就是题主所说的情况。

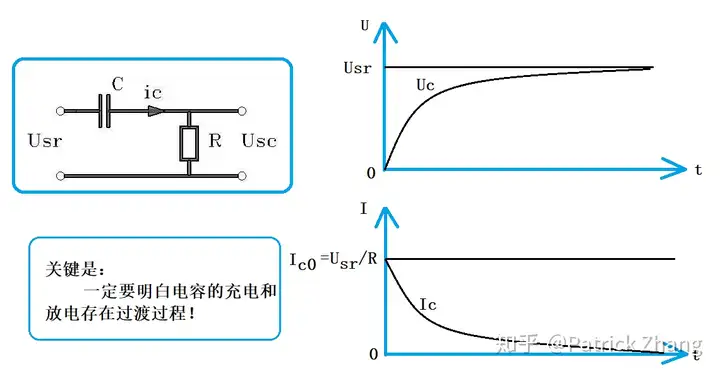
当Usr瞬间加到电容和电阻串联电路上时，因为电容两端的电压不允许突变，此时电容相当于被短路。于是在时刻0，流过电容和电阻R的电流为： IC0=UsrRI_{C0}=\frac{U_{sr}}{R} 。

接着电容开始了充电过程，电流也越来越小。等到了5倍RC的时间后，电容充电基本结束，电流也减小到零。此后，就进入了稳态。

这里的RC叫做时间常数。

我们知道，电阻等于电压与电流之比，即R=U/I。我们还知道，电容C等于电量Q与电压U之比，而电量Q则等于电流I与时间t的乘积，即：

RC=UI×QU=UI×ItU=tRC=\frac{U}{I}\times\frac{Q}{U}=\frac{U}{I}\times\frac{It}{U}=t

原来电阻与电容的乘积就是时间。电阻的单位为欧姆，电容的单位为法拉，则时间的单位就是秒。

图1中，电容充电时，它两端的电压为：

UC=Usr(1−e−tRC)U_C=U{sr}(1-e^{-\frac{t}{RC}}) ，式1。

我们把t=0、1RC、2RC、3RC、4RC和5RC时的Uc求出来，如下：

t=0RC,Uc=Usr(1−1e0)=Usr(1−1)=0Vt=0RC,U_c=U_{sr}(1-\frac{1}{e^{0}})=U_{sr}(1-1)=0V

t=1RC,Uc=Usr(1−0.3678)≈0.6322Usrt=1RC,U_c=U_{sr}(1-0.3678)\approx 0.6322U_{sr}

t=2RC,Uc=Usr(1−0.1353)≈08647Usrt=2RC,U_c=U_{sr}(1-0.1353)\approx 08647U_{sr}

t=3RC,Uc=Usr(1−0.0498)≈0.9512Usrt=3RC,U_c=U_{sr}(1-0.0498)\approx 0.9512U_{sr}

t=4RC,Uc=Usr(1−0.0163)≈0.9837Usrt=4RC,U_c=U_{sr}(1-0.0163)\approx 0.9837U_{sr}

t=5RC,Uc=Usr(1−0.0067)≈0.9933Usrt=5RC,U_c=U_{sr}(1-0.0067)\approx 0.9933U_{sr}

可见，当时间t=0时，电容两端的电压等于零；当t=5RC时，电容两端的电压几乎就等于输入电压。

我们再看流过电容的电流，它的表达式如下：

IC=UsrRe−tRCI_C=\frac{U_{sr}}{R}e^{-\frac{t}{RC}} ，式2

当t=5RC时，有： IC=UsrRe−5RCRC≈0.067×UsrRI_C=\frac{U_{sr}}{R}e^{-\frac{5RC}{RC}}\approx 0.067\times\frac{U_{sr}}{R} 。可见，此时的电流几乎就等于零了。

题主一定要把电容的暂态过程和稳态过程分开来理解，立刻就能得到问题解答。

现在，我们来把以上讨论结果总结一下：

1）电容充电电路存在暂态过程和稳态过程；

2）在电容充电的起始时刻，必须考虑到电容两端的电压不允许突变，这是一个重要原则；

3）暂态过程一般在5RC后就结束了；

4）对于图1，在暂态起始时刻，电容电压Uc等于零，电流Ic等于最大值，我们由欧姆定律可知 UC/IC=0U_C/I_C=0，即电容的等效电阻等于零。我们说，此时电容等效于短路；在暂态结束的稳态时刻，电容电压Uc等于输入电压Usr，而电容电流Ic=0，我们由欧姆定律可知 UC/IC=∞U_C/I_C=\infty ，即电容的等效电阻等于无穷大。我们说，此时电容等效于开路。

5）如果输入信号电压是短暂的脉冲，则电容可以把信号传输到负载端；如果输入信号是不变的恒定电压，则电容仅仅在短暂的过渡过程中有反应，之后便阻隔输入信号；如果输入信号是交流信号，它正好处于上述两种情况的中间。

交流信号的频率越高，就越容易通过电容。我们把这种特性叫做高通滤波器功能。虽然交流信号能够通过电容，但会有一定的削幅。

这说明：稳态下电容具有隔离直流的功能，并且电容具有高通特性。

推而广之，凡是有电容和电感的电路中，一定要按暂态和稳态来分析电路，才能得到准确结论。

最后，我们来看下图：

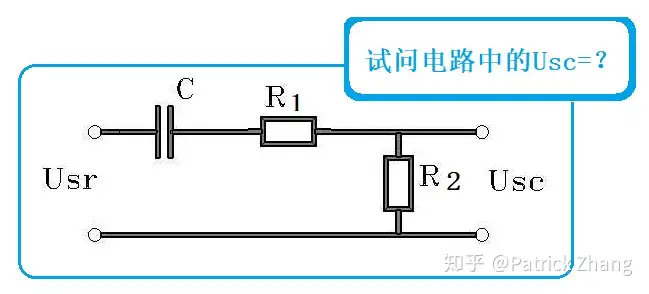
如果我们设Usr=10Vdc，电容等于10微法，电阻R1和R2均为1千欧，请问题主，如何分析Usc的值？

我来解答吧。

第一步，要确认电容的时间常数

我们看下图：

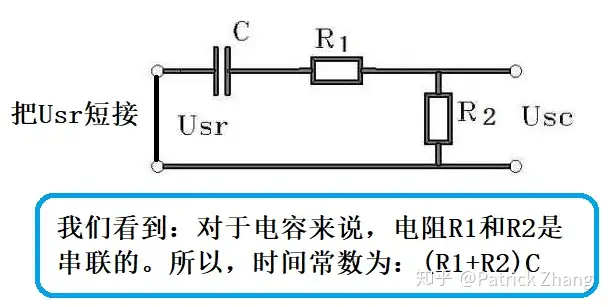
可见，时间常数为 （）(R1+R2)C=（1+1）×103×10×10−6=0.02s(R_1+R_2)C=（1+1）\times 10^3\times 10\times 10^{-6}=0.02s ，也就是20毫秒，5倍时间常数的时间是0.1秒。

第二步，我们来计算Ucs的具体值。

当图2中的Usr刚刚建立时，电容压降等于零，于是有： Usc=UsrR1R1+R2U_{sc}=U_{sr}\frac{R_1}{R_1+R_2} 。

当过了5倍时间常数的时间后，电容充满了电压，其值为Uc=Usr。因此Usc=0。

因此有： Usc=UsrR1R1+R2e−t(R1+R2)CU_{sc}=\frac{U_{sr}R_1}{R_1+R_2}e^{-\frac{t}{(R_1+R_2)C}} 。

当刚刚送电时，t=0： Usc=10×11+1=5VU_{sc}=\frac{10\times 1}{1+1}=5V

当时间过了0.1秒后，我们有： Usc=5×e−5≈0.0337VU_{sc}=5\times e^{-5}\approx 0.0337V ，此时的Usc几乎就等于零了。

解答完毕。

现在，我们把R1与C并联，看看情况又会如何：

我们看下图：

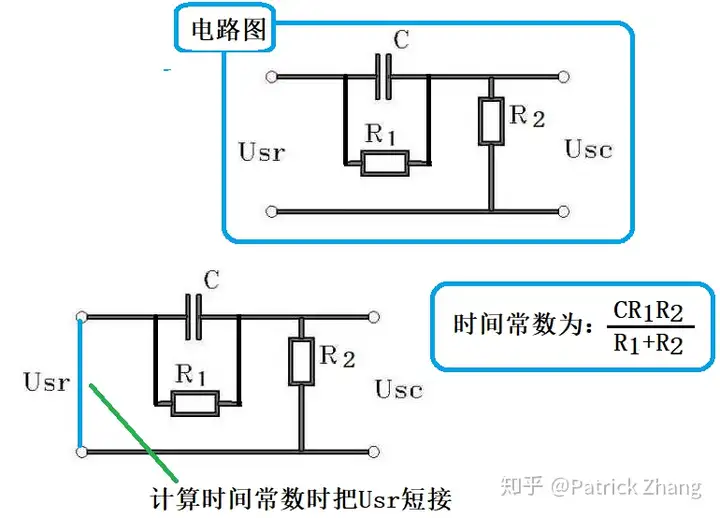
我们看到，把图4中的Usr短路，则R1和R2并联，于是时间常数为： CR1R2R1R2\frac{CR_1R_2}{R_1R_2} 。

当Usr送电伊始，C相当于短接，Usr直接加载在电阻R2的两端，于是此时Usc=Use。

当电路进入稳态时，Usc相当于电阻R2和R1对Usr的分压，即： Usc=UsrR2R1+R2U_{sc}=\frac{U_{sr}R_2}{R_1+R_2} 。

据此，我们就可以列写方程了，如下：

Usc=(Usr−UsrR2R1+R2)e−t(R1+R2)R1+R2+UsrR2R1+R2U_{sc}=(U_{sr}-\frac{U_{sr}R_2}{R_1+R_2})e^{-\frac{t(R_1+R_2)}{R_1+R_2}}+\frac{U_{sr}R_2}{R_1+R_2} 。

上式中，等号右边第一项是电容电压的改变量，体现了过渡过程。等号右边第二项是最终稳态电压。

我们把参数代入，看看结果如何：

先算时间常数： CR1R2R1R2=10×10−6×1×11+1=5×10−6s\frac{CR_1R_2}{R_1R_2}=10\times 10^{-6}\times\frac{1\times1}{1+1}=5\times 10^{-6}s

也就是说，当时间在5倍时间常数即25微秒后，输出电压趋于稳定。最终值为：

Usc=UsrR2R1+R2=10×11+1=5VU_{sc}=\frac{U_{sr}R_2}{R_1+R_2}=\frac{10\times 1}{1+1}=5V

依然是5V，只是过渡过程只有25微秒，比先前的0.1秒大大地提前了。